The Power of the Complex Plane

One day, you find yourself in a dungeon. Looking around, you see the lock to get out. Underneath the lock, there is a puzzle:

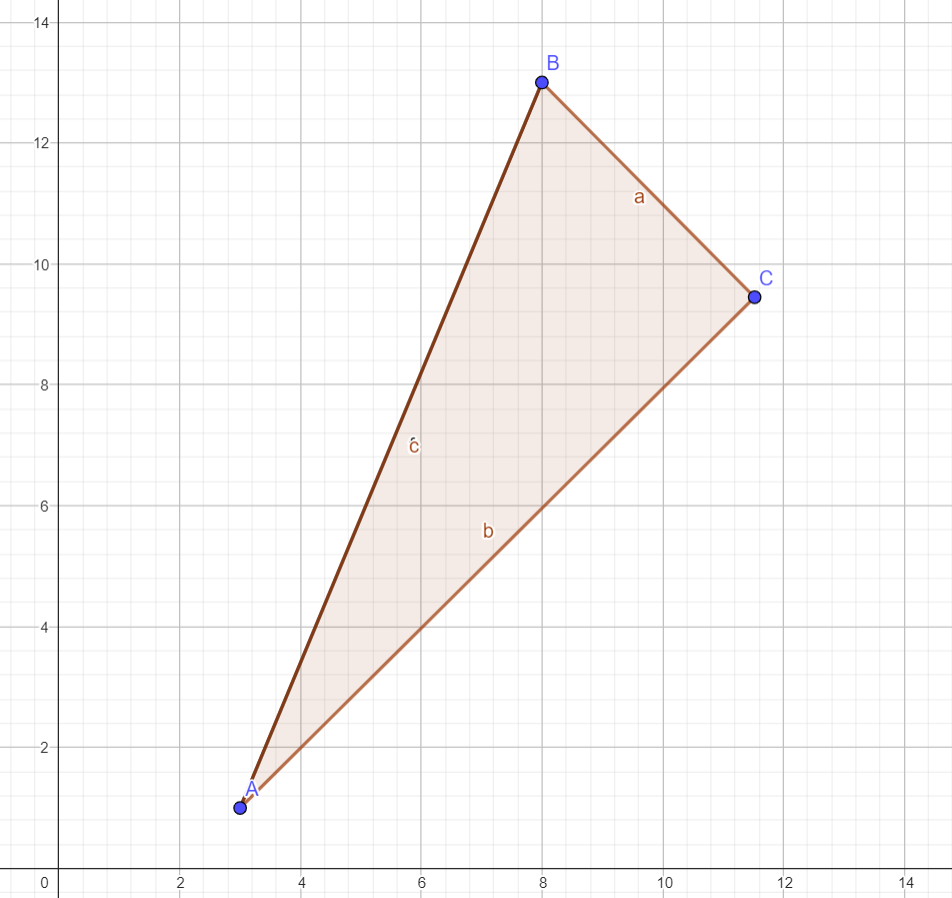
Intrigued by the puzzle, you wonder if there was a way to perform a rotation and dilation on $\overline{AB}$ such that you create $\overline{AC}$⁠, one of the legs of the triangle. Then, it hits you: use the complex plane! The coordinates $(x, y)$ on the coordinate plane correspond to the point $x + yi$ on the complex plane. Namely, the x-value corresponds to the real component and the y-value corresponds to the imaginary component. The point $x+yi$ is written in rectangular form, and has nice properties when dealing with rotations and dilations. For examples, rotations can be dealt with using Euler’s Formula.

Rotations on the Complex Plane

Euler’s Formula states that

$$e^{\theta i} = + i.$$

Unfortunately, a proof of this formula will be beyond the scope of this article.

Let’s say that you have the point $e^{\alpha i}$. In rectangular form, the point is expressed as $+ i$. On the complex plane, this is the same point as the angle $\mathrm{\angle }\alpha$ on the unit circle in the complex plane. To get from angle $\alpha$ to angle $\alpha + \beta$⁠, we need perform a transformation on $e^{\alpha i}$ such that the argument (the angle) becomes $\alpha + \beta$. By complex number multiplication, we multiply $e^{\beta i}$ to $e^{\alpha i}$ to get $e^{(\alpha + \beta) i}$. Thus, to rotate point $e^{\alpha i}$ counterclockwise about the origin by $\mathrm{\angle }\beta$⁠, we multiply it by $e^{\beta i}$⁠, or $+ i$.

Dilations on the Complex Plane

Now, let’s explore dilations. Let’s start again with a point on the complex plane, namely, $me^{\alpha i} = m(cos{\alpha} + i)$. Since the magnitude of $\cos\alpha + i$ is $1$⁠, the magnitude of $m(cos{\alpha} + i)$ is $m$. We want to dilate the point such that the magnitude is now $n$. Thus, we multiply by ${m}$ to get

$${m} |m\cos\alpha + i| &= {m} \cdot m, {m} \cdot me^{\alpha i} &= n.$$

Thus, to dilate a point $me^{\alpha i}$ such that the magnitude becomes $n$⁠, we multiply it by ${m}$.

Solving the Puzzle

With the power of the complex plane, we are able to rotate and then dilate $\overline{AB}$ to create $\overline{AC}$. To rotate $\overline{AB}$⁠, we first transform $\overline{AB}$ such that $A$ lies on the origin. Otherwise, we are rotating $B$ around the origin, instead of $B$ with respect to $A$. Thus, we subtract $(3, 1)$ from all points to get that A’ = (0, 0) and B’ = (5, 12). Then, we translate this onto the complex plane to get that A’ = 0 and B’ = 5+12i.

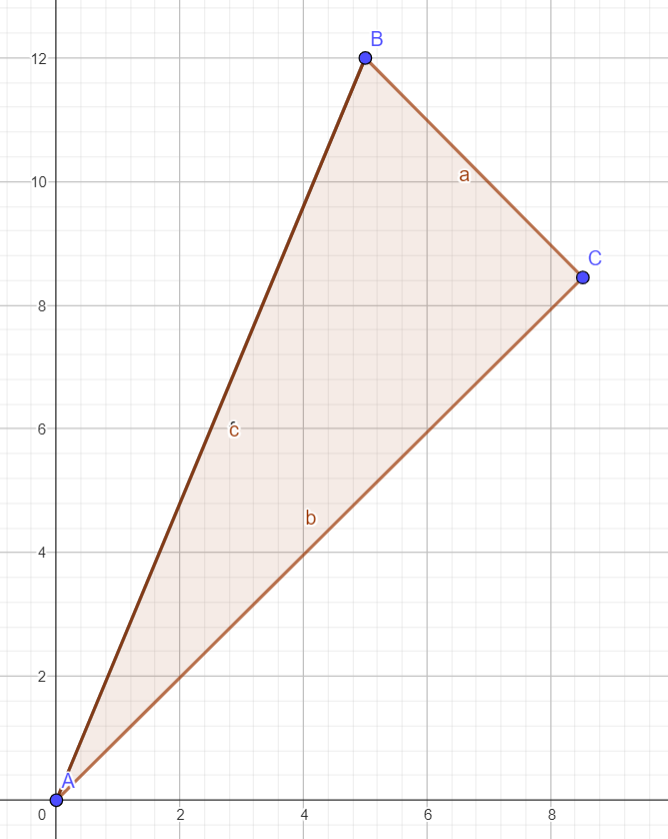
To rotate $\overline{AB}$ to $\overline{AC}$⁠, we need to rotate by angle $\mathrm{\angle }BAC$ clockwise around the origin. Let $\mathrm{\angle }BAC$ be $\theta$. Since $= 90^{\circ}$⁠, $= {13}$ and $= {13}$. However, since we are rotating by an angle clockwise, we are multiplying by $e^{\theta i}$. On the unit circle, a negated angle has the same cosine but opposite sine. Thus, $e^{-\theta i} = - = {13} - {13}i$ . Then, we are multiplying $5 + 12i$ by $e^{-\theta i} = {13} - {13}i$. Simplifying, we get

$$(5+12i)\left({13} - {13}i\right) = {13} + {13}i.$$

Next, we dilate B’ such that magnitude matches that of what C’ should be. Since |B’| = 13 and |C’| = 12⁠, we multiply ${13} + {13}i$ by ${13}$ to get that the coordinates of C’ are

$${169} + {169}i.$$

Lastly, we translate C’ back to the original spot by adding $A$⁠, or $3+i$ to every coordinate to get that the coordinates of $C$ in rectangular form are

$${169} + {169}i.$$

Thus, the coordinates of $C$ on the coordinate plane is $\left({169}, {169}\right)$. Suddenly, a floating iPad comes into existence in front of you, just in time for you to type in the coordinates and open the door. We have conquered a puzzle using the power of the complex plane!